بحث حول التراث الوطني الجزائري

بحث حول الزوايا وقياساتها:

الزوايا

 الزوايا وأنواعها وقياستها :

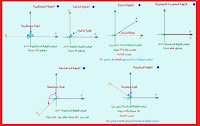
أنواع الزوايا:

1- الزاوية المنعدمة: وهي الزاوية التي ينطبق أحد ضلعيها على الآخر ، ويكون قياسها صفر.
2- الزاوية الحادة: هي الزاوية التي يكون قياسها أكبر من صفر وأقل من 90 درجة.
3- الزاوية القائمة: هي التي يتعامد أحد ضلعيها على الآخر، ويكون قياسها 90 درجة.
4- الزاوية المنفرجة: هي الزاوية التي تزيد درجة قياسها عن 90 وتقل عن 180 درجة.
5- الزاوية المستقيمة: هي التي يقع ضلعاها على استقامة واحدة ، فيكون قياسها 180 درجة.
الزاوية المنعكسة: هي الزاوية التي تزيد درجة قياسها عن 180 وتقل عن 360 درجة.

* هناك أنواع أخرى للزوايا وتعرف بحسب علاقات الزوايا الموجودة في الشكل الهندسي الواحد وعلاقتهم ببعضهما البعض مثل:

* زاويتان متتامتان: هما زاويتان مجموع قياسهما يساوي 90 درجة.
* زاويتان متكاملتان: هما زاويتان مجموع قياسهما يساوي 180 درجة.
* زاويتان متجاورتان: هما زاويتان تشتركان في الرأس وأحد ضلعيهما.
* زاويتان متساويتان: هما زاويتان لهما نفس القياس.
* زاويتان متقابلتان: هما زاويتان تشتركان في نفس الرأس، وأضلاعهما تكون على نفس الامتداد .

طريقة قياس الزوايا المختلفة ووحدة قياسها:

عليك اولاً احضار الأدوات الهندسية التي سوف تساعدك في قياس أو رسم أي شكل هندسي ، وفي حالة قياس الزاوية سيكون عليك استخدام (المنقلة) والقيام بالخطوات التالية :
1- ضع مركز المنقلة بحيث يكون متطابقًا تمامًا مع مركز الزاوية.
2- تأكد من أن الضلع صفر في المنقلة منطبق تمامًا على أحد ضلعي الزاوية.
3- درجة قياس الزاوية هي الدرجة التي يمر بها ضلع الزاوية الآخر.

 وحدات قياس الزاوية:

يتم حسابها بأربعة وحدات قياس وهم ( الدرجة ، الدقيقة ، الثانية ، الراديان ).

المثلثات:

تصنف المثلثات حسب طول أضلاعها كما يلي:

* مثلث متساوي الأضلاع:

 هو مثلث جميع أضلاعه متساوية ، وتكون (جميع زوايا المثلث متساوي الأضلاع متساوية ) ، وقيمة كل منها 60 درجة.

* مثلث متساوي الضلعين:

 ويسمى أيضا متساوي الساقين ، هو مثلث فيه ضلعان متساويان ( الزاويتان المقابلتان لهذين الضلعين تكونان متساويتان أيضا).

* مثلث مختلف الأضلاع: 

هو مثلث أطوال أضلاعه مختلفة ( زوايا هذا المثلث تكون مختلفة القيم أيضا ).

نظرية فيثاغورث لحساب المثلثات:

تعتبر نظرية فيثاغورث هي النظرية الأهم في علوم الرياضيات وحساب المثلثات ، وهي كالتالي:

 في المثلث القائم ، مربع طول الوتر (ا َ) يساوي مجموع مربعي طولي الضلعين القائمين (ب َ، ج َ) ، أي:
أ َ2 = ب َ2 + ج َ2
A2 = B2 + C2
مما يعني أن معرفة طولي ضلعين من المثلث القائم، كافٍ لمعرفة طول الضلع الثالث.

من الممكن تعميم نظرية فيثاغورث لتشمل أي مثلث عبر قانون جيب التمام، حيث:

مربع طول الضلع = مجموع مربعي الضلعين الآخرين مطروح منه ضعف حاصل ضروب طولي الضلعين الآخرين في جيب تمام ( الزاوية المحصورة بينهما ) .
|أ|^2 = |ب|^2 + |ج|^2 – 2 × |ب|× |ج| × جتا (دْ)
A2 = B2 + C2 − 2 * B * C * cosα
و هو صحيح لكل المثلثات حتى ولو لم تكن الزاوية (د) قائمة.